Implementing Davenport

This is the fourth in a series of posts about the development of socelect.org. Find the first here, introducing socelect.

Motivation

By now, having read the previous post you have an idea what excites me about Kemeny orders and Davenport’s algorithm.

What I felt was missing was a good implementation. By “good” I mean, easy to integrate into your application, fast, correct, and reliable. I felt it possible to implement without dependencies on much more than a C compiler and linker and the standard libraries.

Assay

Before starting I satisfied myself that I wasn’t reinventing the wheel simply to divert myself with an enjoyable project, which is not to say that the motivation of diversion is not valid or sufficient. I did an assay of the existing state of the art.

• The paper from Davenport and Conitzer in which they develop the strongest lower bound contains an “integer formulation” of the solution that can be used with constraint solving programs. I tried it with the free edition of IBM’s CPLEX and found that it worked. All I needed to do was license and install CPLEX everywhere I wanted to use it, e.g. in judged sport analysis or in socelect.

• There is a Wikipedia page about the method, which contained links to two other implementations. The first is in C++, which is promising. It as a program published on Numerical Recipes, a resource that I’ve always respected and enjoyed. There are some aspects of the implementation that I’m not happy with:
  • It requires purchase of a license
  • It uses the heuristic, but not the strong lower bound of Davenport’s algorithm.
  • It uses an outer loop that tries a given number of possibilities. It is not exhaustive.

  To be fair, there are contrived cases where the exhaustive search can lead to impractical run times; and, the heuristic is very powerful.

• An implementation of the integer formulation in Python. This Rank Aggregation post does something near and dear to me. It applies the method to a judged sport result. I really love that post. The implementation
  • uses the integer formulation, not the branch and bound search.
  • requires installing the lpsolve library.
• The original implementation that Davenport and Conitzer used is proprietary to IBM and not published. I know that it used the boost C++ library.

It’s likely I did it because I wanted to, for the challenge; however, the assay showed that the contribution is something new– an open-source implementation of the complete branch and bound search algorithm, using the strong lower bounds, that stands alone without need for installing a large library.

Coding in C

After taking a break to provide the International Aerobatic Club (IAC) some updates to the results system that I develop and maintain for them, work on this started the second week of April this year (2019).

Coding in C is a joy. C (or C++) is so fundamental to computing (many operating systems, including Linux, Windows, and MacOS are coded with it) that great compilers for it are common.

Building the project

It has been about twenty years since I wrote more than a short C program. The new-to-me thing about writing a C program was the presence of an excellent build system from the GNU project, autoconf and automake. Learning to use these took substantial time and effort, however worthwhile because:

• They remove the need to manually write a build, generally with a make file
• They provide the bonus of making the project work on just about any operating system where you want to build it.

Testing the project

Coding with any language is fraught with danger, my opinion, if not undertaken testing first. Searching for a testing framework for C, I found that I favor Cutter and to a lesser extent Check. I initially had trouble with Cutter, and started with Check. Resolving the trouble I had with Cutter through this interaction with the developers, for which I’m very grateful, I found great satisfaction with testing the library using Cutter.

The Cutter tests are just C functions with assertions. It’s possible to run the tests by directory or to run a single test function. It isn’t necessary to build test suites. The output results are clear. Providing good outputs is essential, and something that takes some significant work that I could not achieve by writing my own set of assertion macros. Cutter turned out to be just right. I could place print statements in the tests and see them in the test output. Using it, other than getting it to work in the first place, was simple as can be.

Majority Preferences

The majority graph, described in the last post, has nodes representing alternatives, and directed edges representing majority preference between each pair of alternatives. A directed edge from Ace to Rickie, for example, with weight 20, represents twenty more preferences that favor Ace over Rickie than favor Rickie over Ace.

A connected component represents a cycle of majority preferences that needs to be broken. In the example, Budd, Cooter, and Rickie are in a connected component. We must break one of the majority preferences in order to place any of them before the other.

By inspection, it’s pretty easy to see that we’re going to break the majority for Budd over Rickie, because that will cause the fewest disagreements; but, we need to teach the computer to do it.

Preflow Push

The most difficult thing, for me, about Davenport’s algorithm is the need to solve a network flow problem in order to compute the strong lower bound. The paper with Conitzer formulates the task in the most straightforward way. What’s needed is an implementation.

Maximum flow is simply this: given a network of nodes like the majority graph and treating the weights on the arcs as capacities, what is the most that can be shipped from a source node to a sink node?

The preflow-push maximum flow algorithm requires its own backtracking search and careful book-keeping. The references that explain it are good. The one I found most useful was the Push–relabel maximum flow algorithm article on Wikipedia, which includes a sample C implementation. (May the gods bless Wikipedia and the people who edit it. Send your donation.)

I went about reproducing the sample implementation with tests, and later optimized it for my use case by enabling the algorithm to run with specified start and end nodes, and specified pre-existing flow. It also uses the optimized data structures I set-up to model the network.

This to me was one of the riskier parts of the project. Having it accomplished was very encouraging. Find the implementation as preflow_push.c and the code that sets-up the network and uses preflow push to compute the lower bound as lower_bound.c.

Tarjan

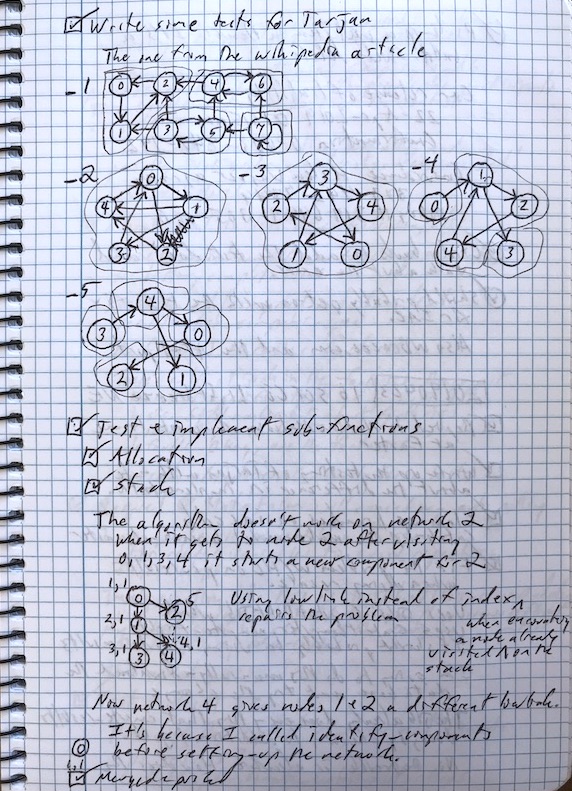
The next part needed by Davenport’s algorithm is a method for finding connected components in the majority graph representing the preferences, and to identify a topological sort.

A topological sort provides the magic that allows us to place the alternatives one before the other in order of preference. In the example majority graph above, it’s easy to see that Ace comes first, followed by the component that includes Budd, Cooter, and Rickie. When we remove the edge connecting Budd to Rickie, the sort is complete. It has no components with more than one alternative. It is Ace, then Rickie, then Cooter, then Budd.

Wikipedia to the rescue again. I found this presentation of Tarjan’s algorithm that contains a reference to the original paper and the pseudocode implementation from that paper.

With careful testing, the implementation was a mere matter of programming. Find it as tarjan.c.

Sorting

The algorithm requires sorting in two places. One place rearranges the results of running Tarjan’s algorithm to arrange alternatives in order of the indexes returned by the topological sort. The other sorts the edges from a component of the majority graph in order of decreasing weight, so as to implement the heuristic that tries edges with the strongest majorities before those with weaker ones.

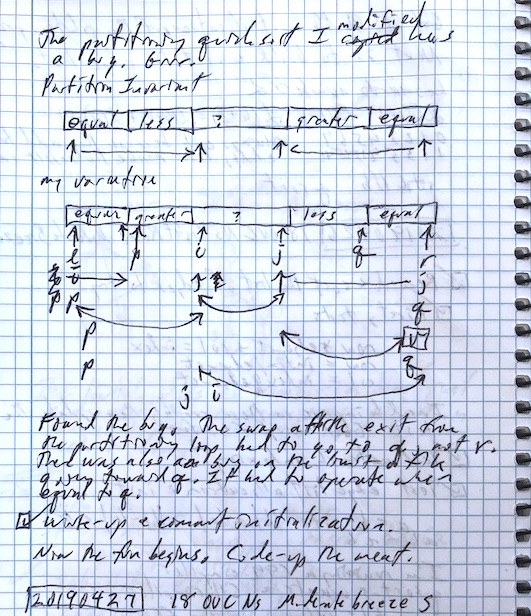
You would think that there’s a system sort available in standard C, but I didn’t find it. The system sort is usually an implementation of the quicksort algorithm. I used quicksort with 3-way partitioning copied from a pdf of a presentation by two famous computer scientists– Robert Sedgewick and Jon Bentley – and published on Sedgewick’s personal pages at Princeton University: Quicksort Is Optimal (pdf). Bentley wrote a book called Programming Pearls, a classic exploration of problem solving using a computer. Sedgewick is a genius about algorithms who did his Ph.D. thesis about quicksort, supervised by Donald Knuth at Stanford. We owe a lot to Stanford.

I modified the code given in the quicksort presentation to enable indirection of value lookup and reverse sorting (high to low). It is twenty lines of tight, tricky code that you’ll find in sorting.c.

Putting it together

Having the dependencies ready, it was time to implement the Davenport algorithm proper, and properly.

The algorithm is a systematic exploration of the problem space guided by the maximum majority heuristic. It represents the current, trial solution as a “solution graph” and checks the lower bound before adding an alternative (descending). Finding a solution, or finding a partial solution that bears no further examination, it backtracks (ascends) to remove the last tried alternative and try other ones. It finishes when it has explored the entire solution space, ruling out large portions that need not be explored.

The implementation uses recursive descent to explore the solution space, and a smallest possible stack recording added edges, that rolls and then unrolls changes to the solution graph. When selecting an edge from the majority graph to add to the solution graph, it computes a “transitive closure” for the solution and checks the majority graph for broken majorities, adding those to the cost of the solution.

The transitive closure is simply this: If we add Rickie before Cooter, and Cooter is already before Budd, then Rickie is before Budd, and we have broken the majority favoring Budd over Rickie. Moreover, if Ace was already before Rickie, then Ace is now before Cooter and Budd as well. Transitive closure simply takes care of the implications of putting any one alternative before another.

As you see, there’s some book-keeping involved. The development strategy was to implement the heuristic search first, then add the test for lower bound.

When adding the test for lower bound, I encountered a crisis. One cold, overcast day in early May, one of the tests for the lower bound would not terminate. The trouble was in updates to the network fed into the preflow-push maximum flow computation. It was only a day, but a long day of uncertainty.

The core implementation is in davenport.c.

Aggregating solutions

The original 1959 paper from Kemeny considers partial orders as well as total orderings of the alternatives. It presents a method of squaring the distances in order to find a unique, partial order solution when there is no majority preference for one alternative over another.

Davenport’s algorithm does not try partial order solutions. To do so would expand the search space considerably. It does not square distances because it isn’t considering partial orders. (Further, it isn’t computing with distances; it’s computing with majorities.)

What Davenport’s algorithm does, is output multiple solutions in these cases, all of which have equal, minimal distance. This is anticipated by Kemeny, and the interpretation he gives is that it implies a partial ordering in which two or more alternatives cannot be said to be preferred one over another.

In the example illustrated, three preferences over five alternatives are expressed. The preferences are:

• Ace, Budd, Cooter, Doc, Rickie;
• Ace, Cooter, Doc, Budd, Rickie; and
• Ace, Doc, Budd, Cooter, Rickie.

Davenport’s algorithm will produce three solutions of equal number of disagreements. In this particular case, the three solutions match the three expressed preferences. The algorithm has output all of the orderings in which two of Budd before Cooter, Cooter before Doc, and Doc before Budd are satisfied.

You might say that the algorithm hasn’t done anything useful. However, interpreting the result as Kemeny does, we can recognize that Ace is preferred to Budd, Cooter, and Doc, none of which is preferred over the others, and then all are preferred over Rickie. (Sorry, Rickie)

To make that interpretation, the code in aggregate_solution.c builds-up a new preference graph from the multiple solutions. It then uses the Tarjan algorithm to identify strongly connected components and a topological sort of those components. The result is a partial order, minimal disagreements solution that matches the one achieved by Kemeny.

Memory management

C does not have a garbage collector. It requires allocating storage and later freeing it. Thus, writing in C presents the following difficulties:

• Memory leaks occur when allocated storage is not later freed. These cause programs to use more and more memory until the amount of memory available is exhausted, or exceeds the capacity of the operating system to manage efficiently for the program.
• Memory overruns occur when the program writes to memory locations that it hasn’t reserved for itself. These cause programs to fail in mysterious ways that are very hard to debug.

Accordingly, one key to successful C programs is careful memory management. The code achieves this by using a mix of object-oriented and functional techniques.

• All allocations happen within a function that creates a named structure.
• All frees happen within a corresponding function that destroys the named structure.
• The allocated structures are used either:
  • within another allocated structure, which both allocates and frees it; or
  • within a function which creates, uses, and then frees it.
• All code that accesses allocated memory is in functions that work with the named structure, and which use the same encapsulated constants or state variables used to allocate the storage to also limit writes to it.

This strategy works very well for me.

Conclusion

Using C was a true joy. One thing that never ceased to astonish me is how fast it has become. My work brought me from C to Java and later Ruby and some other interpreted languages. This meant that, while I saw computation getting faster, I didn’t have an apples-to-apples view of the change. Some of the speed gains were swallowed-up by the interpreters I was using, which were themselves made practical by the speed gains.

Coming back to C after all these years, the computation speed increases came to life. The tests ask the computer to do hundreds of thousands, maybe millions of computations. Running them on my MacBook Pro happens in the blink of an eye. More than once I had to satisfy myself that it was actually running the tests!

The implementation was complete on the fifteenth of May, after about five weeks of intense work. You can find the complete project, including source as wbreeze/davenport on GitHub.

It was something I had wanted to do for about fifteen years, that was often in the back of my mind. Knowing that, I had to do it. It was both a relief and a source of great satisfaction to have it accomplished.